extern/rclone
1
0
Fork 0
mirror of https://github.com/rclone/rclone.git synced 2024-12-23 07:29:35 +01:00
Code Issues Packages Projects Releases Wiki Activity

vendor: remove github.com/VividCortex/ewma dependency

Browse Source
This commit is contained in:
Nick Craig-Wood 2018-06-11 11:31:18 +01:00
parent ca44fb1fba
commit 502d8b0cdd
8 changed files with 0 additions and 421 deletions
Show Stats Download Patch File Download Diff File Expand all files Collapse all files

9
Gopkg.lock generated
View File

@ -56,14 +56,6 @@
pruneopts = ""
revision = "ef1e4c783f8f0478bd8bff0edb3dd0bade552599"
[[projects]]
digest = "1:ac226c42eb54c121e0704c6f7f64c96c7817ad6d6286e5536e8cea72807e1079"
name = "github.com/VividCortex/ewma"
packages = ["."]
pruneopts = ""
revision = "b24eb346a94c3ba12c1da1e564dbac1b498a77ce"
version = "v1.1.1"
[[projects]]
branch = "master"
digest = "1:391632fa3a324c4f461f28baaf45cea8b21e13630b00f27059613f855bb544bb"
@ -580,7 +572,6 @@
"github.com/Azure/go-ansiterm",
"github.com/Azure/go-ansiterm/winterm",
"github.com/Unknwon/goconfig",
"github.com/VividCortex/ewma",
"github.com/a8m/tree",
"github.com/abbot/go-http-auth",
"github.com/aws/aws-sdk-go/aws",

10
vendor/github.com/VividCortex/ewma/.github/ISSUE_TEMPLATE.md generated vendored
View File

@ -1,10 +0,0 @@
Before you file an issue, please consider:
We only accept pull requests for minor fixes or improvements. This includes:
* Small bug fixes
* Typos
* Documentation or comments
Please open issues to discuss new features. Pull requests for new features will be rejected,
so we recommend forking the repository and making changes in your fork for your use case.

10
vendor/github.com/VividCortex/ewma/.github/PULL_REQUEST_TEMPLATE.md generated vendored
View File

@ -1,10 +0,0 @@
Before you create a pull request, please consider:
We only accept pull requests for minor fixes or improvements. This includes:
* Small bug fixes
* Typos
* Documentation or comments
Please open issues to discuss new features. Pull requests for new features will be rejected,
so we recommend forking the repository and making changes in your fork for your use case.

2
vendor/github.com/VividCortex/ewma/.gitignore generated vendored
View File

@ -1,2 +0,0 @@
.DS_Store
.*.sw?

21
vendor/github.com/VividCortex/ewma/LICENSE generated vendored
View File

@ -1,21 +0,0 @@
The MIT License
Copyright (c) 2013 VividCortex
Permission is hereby granted, free of charge, to any person obtaining a copy
of this software and associated documentation files (the "Software"), to deal
in the Software without restriction, including without limitation the rights
to use, copy, modify, merge, publish, distribute, sublicense, and/or sell
copies of the Software, and to permit persons to whom the Software is
furnished to do so, subject to the following conditions:
The above copyright notice and this permission notice shall be included in
all copies or substantial portions of the Software.
THE SOFTWARE IS PROVIDED "AS IS", WITHOUT WARRANTY OF ANY KIND, EXPRESS OR
IMPLIED, INCLUDING BUT NOT LIMITED TO THE WARRANTIES OF MERCHANTABILITY,
FITNESS FOR A PARTICULAR PURPOSE AND NONINFRINGEMENT. IN NO EVENT SHALL THE
AUTHORS OR COPYRIGHT HOLDERS BE LIABLE FOR ANY CLAIM, DAMAGES OR OTHER
LIABILITY, WHETHER IN AN ACTION OF CONTRACT, TORT OR OTHERWISE, ARISING FROM,
OUT OF OR IN CONNECTION WITH THE SOFTWARE OR THE USE OR OTHER DEALINGS IN
THE SOFTWARE.

140
vendor/github.com/VividCortex/ewma/README.md generated vendored
View File

@ -1,140 +0,0 @@
# EWMA [![GoDoc](https://godoc.org/github.com/VividCortex/ewma?status.svg)](https://godoc.org/github.com/VividCortex/ewma) ![Build Status](https://circleci.com/gh/VividCortex/moving_average.png?circle-token=1459fa37f9ca0e50cef05d1963146d96d47ea523)
This repo provides Exponentially Weighted Moving Average algorithms, or EWMAs for short, [based on our
Quantifying Abnormal Behavior talk](https://vividcortex.com/blog/2013/07/23/a-fast-go-library-for-exponential-moving-averages/).
### Exponentially Weighted Moving Average
An exponentially weighted moving average is a way to continuously compute a type of
average for a series of numbers, as the numbers arrive. After a value in the series is
added to the average, its weight in the average decreases exponentially over time. This
biases the average towards more recent data. EWMAs are useful for several reasons, chiefly
their inexpensive computational and memory cost, as well as the fact that they represent
the recent central tendency of the series of values.
The EWMA algorithm requires a decay factor, alpha. The larger the alpha, the more the average
is biased towards recent history. The alpha must be between 0 and 1, and is typically
a fairly small number, such as 0.04. We will discuss the choice of alpha later.
The algorithm works thus, in pseudocode:
1. Multiply the next number in the series by alpha.
2. Multiply the current value of the average by 1 minus alpha.
3. Add the result of steps 1 and 2, and store it as the new current value of the average.
4. Repeat for each number in the series.
There are special-case behaviors for how to initialize the current value, and these vary
between implementations. One approach is to start with the first value in the series;
another is to average the first 10 or so values in the series using an arithmetic average,
and then begin the incremental updating of the average. Each method has pros and cons.
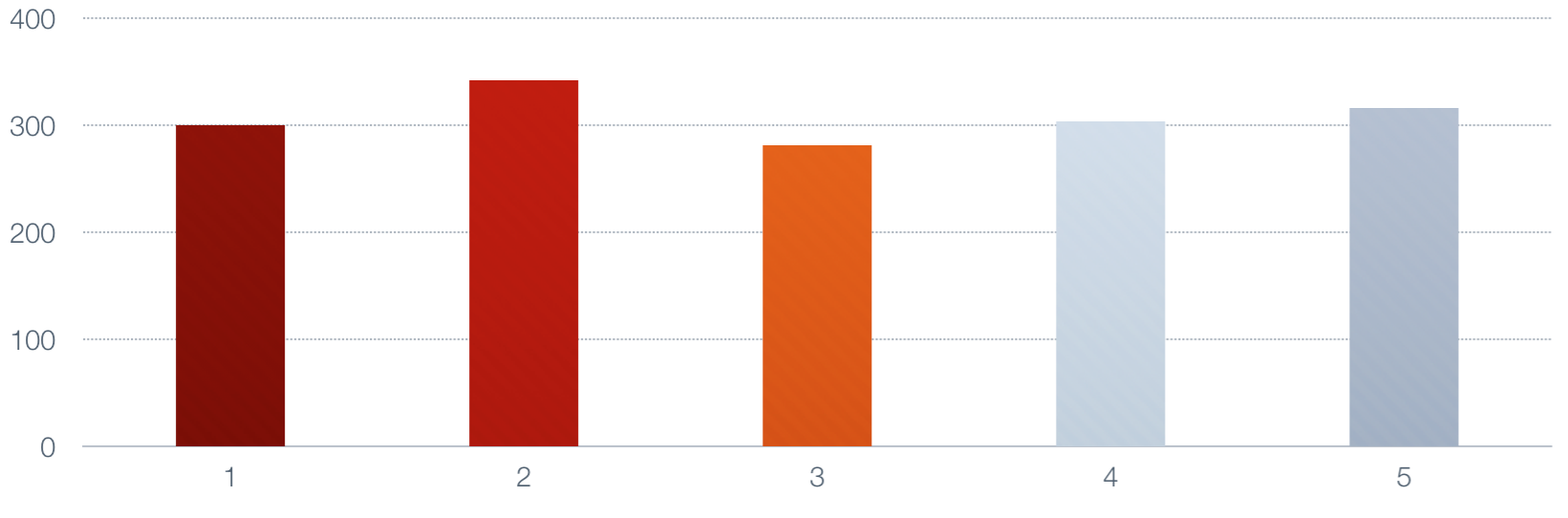
It may help to look at it pictorially. Suppose the series has five numbers, and we choose
alpha to be 0.50 for simplicity. Here's the series, with numbers in the neighborhood of 300.
![Data Series](https://user-images.githubusercontent.com/279875/28242350-463289a2-6977-11e7-88ca-fd778ccef1f0.png)
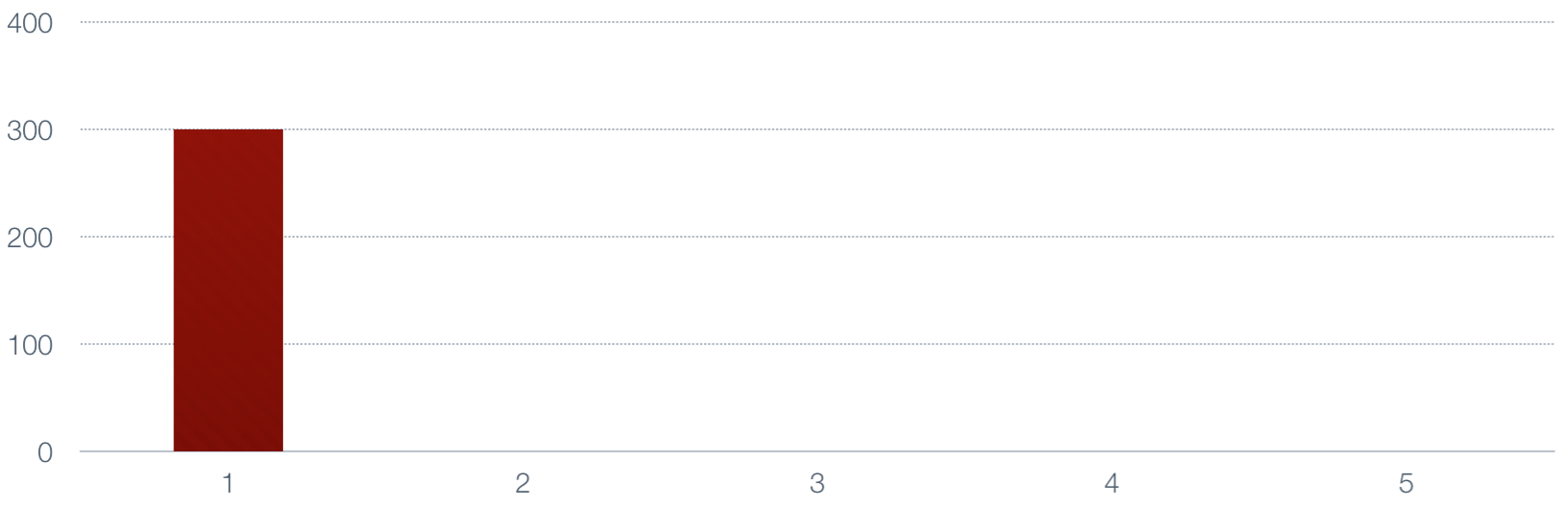
Now let's take the moving average of those numbers. First we set the average to the value
of the first number.
![EWMA Step 1](https://user-images.githubusercontent.com/279875/28242353-464c96bc-6977-11e7-9981-dc4e0789c7ba.png)
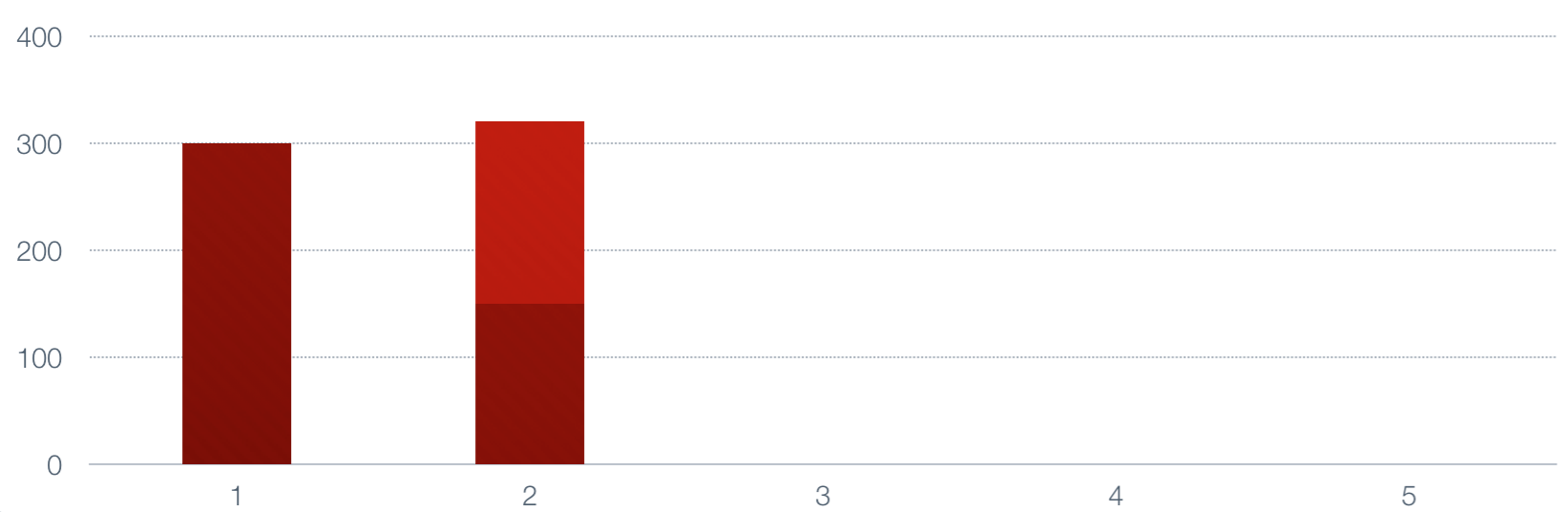
Next we multiply the next number by alpha, multiply the current value by 1-alpha, and add
them to generate a new value.
![EWMA Step 2](https://user-images.githubusercontent.com/279875/28242351-464abefa-6977-11e7-95d0-43900f29bef2.png)
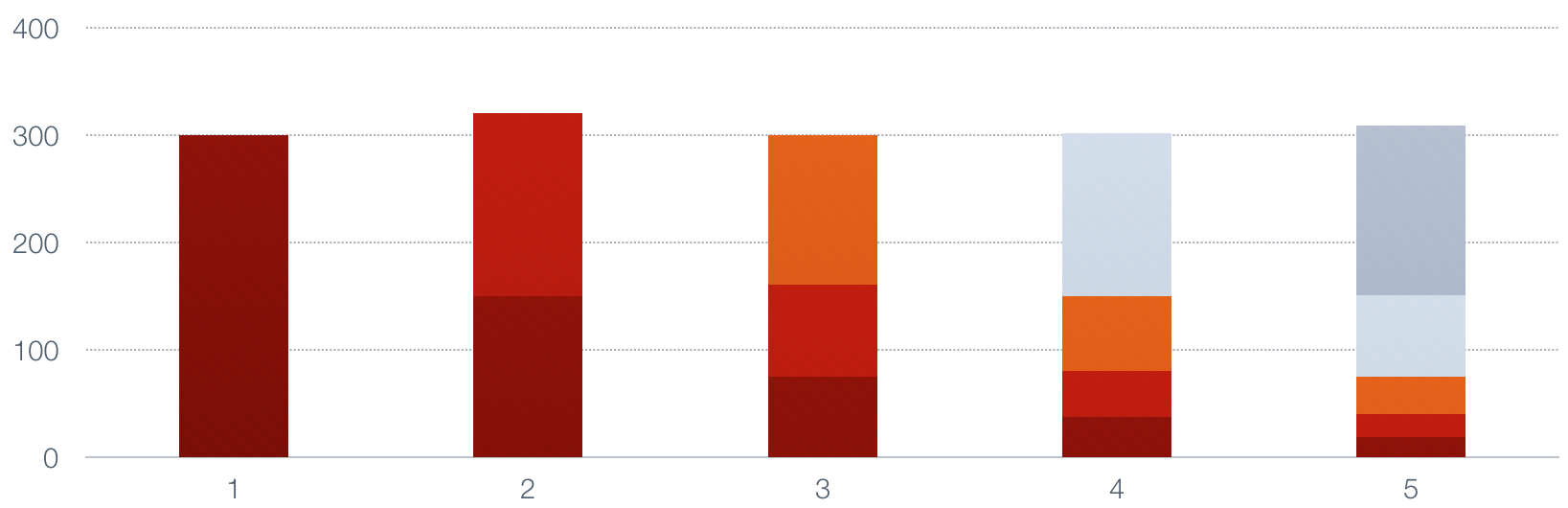
This continues until we are done.
![EWMA Step N](https://user-images.githubusercontent.com/279875/28242352-464c58f0-6977-11e7-8cd0-e01e4efaac7f.png)
Notice how each of the values in the series decays by half each time a new value
is added, and the top of the bars in the lower portion of the image represents the
size of the moving average. It is a smoothed, or low-pass, average of the original
series.
For further reading, see [Exponentially weighted moving average](http://en.wikipedia.org/wiki/Moving_average#Exponential_moving_average) on wikipedia.
### Choosing Alpha
Consider a fixed-size sliding-window moving average (not an exponentially weighted moving average)
that averages over the previous N samples. What is the average age of each sample? It is N/2.
Now suppose that you wish to construct a EWMA whose samples have the same average age. The formula
to compute the alpha required for this is: alpha = 2/(N+1). Proof is in the book
"Production and Operations Analysis" by Steven Nahmias.
So, for example, if you have a time-series with samples once per second, and you want to get the
moving average over the previous minute, you should use an alpha of .032786885. This, by the way,
is the constant alpha used for this repository's SimpleEWMA.
### Implementations
This repository contains two implementations of the EWMA algorithm, with different properties.
The implementations all conform to the MovingAverage interface, and the constructor returns
that type.
Current implementations assume an implicit time interval of 1.0 between every sample added.
That is, the passage of time is treated as though it's the same as the arrival of samples.
If you need time-based decay when samples are not arriving precisely at set intervals, then
this package will not support your needs at present.
#### SimpleEWMA
A SimpleEWMA is designed for low CPU and memory consumption. It **will** have different behavior than the VariableEWMA
for multiple reasons. It has no warm-up period and it uses a constant
decay. These properties let it use less memory. It will also behave
differently when it's equal to zero, which is assumed to mean
uninitialized, so if a value is likely to actually become zero over time,
then any non-zero value will cause a sharp jump instead of a small change.
#### VariableEWMA
Unlike SimpleEWMA, this supports a custom age which must be stored, and thus uses more memory.
It also has a "warmup" time when you start adding values to it. It will report a value of 0.0
until you have added the required number of samples to it. It uses some memory to store the
number of samples added to it. As a result it uses a little over twice the memory of SimpleEWMA.
## Usage
### API Documentation
View the GoDoc generated documentation [here](http://godoc.org/github.com/VividCortex/ewma).
```go
package main
import "github.com/VividCortex/ewma"
func main() {
samples := [100]float64{
4599, 5711, 4746, 4621, 5037, 4218, 4925, 4281, 5207, 5203, 5594, 5149,
}
e := ewma.NewMovingAverage() //=> Returns a SimpleEWMA if called without params
a := ewma.NewMovingAverage(5) //=> returns a VariableEWMA with a decay of 2 / (5 + 1)
for _, f := range samples {
e.Add(f)
a.Add(f)
}
e.Value() //=> 13.577404704631077
a.Value() //=> 1.5806140565521463e-12
}
```
## Contributing
We only accept pull requests for minor fixes or improvements. This includes:
* Small bug fixes
* Typos
* Documentation or comments
Please open issues to discuss new features. Pull requests for new features will be rejected,
so we recommend forking the repository and making changes in your fork for your use case.
## License
This repository is Copyright (c) 2013 VividCortex, Inc. All rights reserved.
It is licensed under the MIT license. Please see the LICENSE file for applicable license terms.

126
vendor/github.com/VividCortex/ewma/ewma.go generated vendored
View File

@ -1,126 +0,0 @@
// Package ewma implements exponentially weighted moving averages.
package ewma
// Copyright (c) 2013 VividCortex, Inc. All rights reserved.
// Please see the LICENSE file for applicable license terms.
const (
// By default, we average over a one-minute period, which means the average
// age of the metrics in the period is 30 seconds.
AVG_METRIC_AGE float64 = 30.0
// The formula for computing the decay factor from the average age comes
// from "Production and Operations Analysis" by Steven Nahmias.
DECAY float64 = 2 / (float64(AVG_METRIC_AGE) + 1)
// For best results, the moving average should not be initialized to the
// samples it sees immediately. The book "Production and Operations
// Analysis" by Steven Nahmias suggests initializing the moving average to
// the mean of the first 10 samples. Until the VariableEwma has seen this
// many samples, it is not "ready" to be queried for the value of the
// moving average. This adds some memory cost.
WARMUP_SAMPLES uint8 = 10
)
// MovingAverage is the interface that computes a moving average over a time-
// series stream of numbers. The average may be over a window or exponentially
// decaying.
type MovingAverage interface {
Add(float64)
Value() float64
Set(float64)
}
// NewMovingAverage constructs a MovingAverage that computes an average with the
// desired characteristics in the moving window or exponential decay. If no
// age is given, it constructs a default exponentially weighted implementation
// that consumes minimal memory. The age is related to the decay factor alpha
// by the formula given for the DECAY constant. It signifies the average age
// of the samples as time goes to infinity.
func NewMovingAverage(age ...float64) MovingAverage {
if len(age) == 0 || age[0] == AVG_METRIC_AGE {
return new(SimpleEWMA)
}
return &VariableEWMA{
decay: 2 / (age[0] + 1),
}
}
// A SimpleEWMA represents the exponentially weighted moving average of a
// series of numbers. It WILL have different behavior than the VariableEWMA
// for multiple reasons. It has no warm-up period and it uses a constant
// decay. These properties let it use less memory. It will also behave
// differently when it's equal to zero, which is assumed to mean
// uninitialized, so if a value is likely to actually become zero over time,
// then any non-zero value will cause a sharp jump instead of a small change.
// However, note that this takes a long time, and the value may just
// decays to a stable value that's close to zero, but which won't be mistaken
// for uninitialized. See http://play.golang.org/p/litxBDr_RC for example.
type SimpleEWMA struct {
// The current value of the average. After adding with Add(), this is
// updated to reflect the average of all values seen thus far.
value float64
}
// Add adds a value to the series and updates the moving average.
func (e *SimpleEWMA) Add(value float64) {
if e.value == 0 { // this is a proxy for "uninitialized"
e.value = value
} else {
e.value = (value * DECAY) + (e.value * (1 - DECAY))
}
}
// Value returns the current value of the moving average.
func (e *SimpleEWMA) Value() float64 {
return e.value
}
// Set sets the EWMA's value.
func (e *SimpleEWMA) Set(value float64) {
e.value = value
}
// VariableEWMA represents the exponentially weighted moving average of a series of
// numbers. Unlike SimpleEWMA, it supports a custom age, and thus uses more memory.
type VariableEWMA struct {
// The multiplier factor by which the previous samples decay.
decay float64
// The current value of the average.
value float64
// The number of samples added to this instance.
count uint8
}
// Add adds a value to the series and updates the moving average.
func (e *VariableEWMA) Add(value float64) {
switch {
case e.count < WARMUP_SAMPLES:
e.count++
e.value += value
case e.count == WARMUP_SAMPLES:
e.count++
e.value = e.value / float64(WARMUP_SAMPLES)
e.value = (value * e.decay) + (e.value * (1 - e.decay))
default:
e.value = (value * e.decay) + (e.value * (1 - e.decay))
}
}
// Value returns the current value of the average, or 0.0 if the series hasn't
// warmed up yet.
func (e *VariableEWMA) Value() float64 {
if e.count <= WARMUP_SAMPLES {
return 0.0
}
return e.value
}
// Set sets the EWMA's value.
func (e *VariableEWMA) Set(value float64) {
e.value = value
if e.count <= WARMUP_SAMPLES {
e.count = WARMUP_SAMPLES + 1
}
}

103
vendor/github.com/VividCortex/ewma/ewma_test.go generated vendored
View File

@ -1,103 +0,0 @@
package ewma
// Copyright (c) 2013 VividCortex, Inc. All rights reserved.
// Please see the LICENSE file for applicable license terms.
import (
"math"
"testing"
)
const testMargin = 0.00000001
var samples = [100]float64{
4599, 5711, 4746, 4621, 5037, 4218, 4925, 4281, 5207, 5203, 5594, 5149,
4948, 4994, 6056, 4417, 4973, 4714, 4964, 5280, 5074, 4913, 4119, 4522,
4631, 4341, 4909, 4750, 4663, 5167, 3683, 4964, 5151, 4892, 4171, 5097,
3546, 4144, 4551, 6557, 4234, 5026, 5220, 4144, 5547, 4747, 4732, 5327,
5442, 4176, 4907, 3570, 4684, 4161, 5206, 4952, 4317, 4819, 4668, 4603,
4885, 4645, 4401, 4362, 5035, 3954, 4738, 4545, 5433, 6326, 5927, 4983,
5364, 4598, 5071, 5231, 5250, 4621, 4269, 3953, 3308, 3623, 5264, 5322,
5395, 4753, 4936, 5315, 5243, 5060, 4989, 4921, 4480, 3426, 3687, 4220,
3197, 5139, 6101, 5279,
}
func withinMargin(a, b float64) bool {
return math.Abs(a-b) <= testMargin
}
func TestSimpleEWMA(t *testing.T) {
var e SimpleEWMA
for _, f := range samples {
e.Add(f)
}
if !withinMargin(e.Value(), 4734.500946466118) {
t.Errorf("e.Value() is %v, wanted %v", e.Value(), 4734.500946466118)
}
e.Set(1.0)
if e.Value() != 1.0 {
t.Errorf("e.Value() is %d", e.Value())
}
}
func TestVariableEWMA(t *testing.T) {
e := NewMovingAverage(30)
for _, f := range samples {
e.Add(f)
}
if !withinMargin(e.Value(), 4734.500946466118) {
t.Errorf("e.Value() is %v, wanted %v", e.Value(), 4734.500946466118)
}
e.Set(1.0)
if e.Value() != 1.0 {
t.Errorf("e.Value() is %d", e.Value())
}
}
func TestVariableEWMA2(t *testing.T) {
e := NewMovingAverage(5)
for _, f := range samples {
e.Add(f)
}
if !withinMargin(e.Value(), 5015.397367486725) {
t.Errorf("e.Value() is %v, wanted %v", e.Value(), 5015.397367486725)
}
}
func TestVariableEWMAWarmup(t *testing.T) {
e := NewMovingAverage(5)
for i, f := range samples {
e.Add(f)
// all values returned during warmup should be 0.0
if uint8(i) < WARMUP_SAMPLES {
if e.Value() != 0.0 {
t.Errorf("e.Value() is %v, expected %v", e.Value(), 0.0)
}
}
}
e = NewMovingAverage(5)
e.Set(5)
e.Add(1)
if e.Value() >= 5 {
t.Errorf("e.Value() is %d, expected it to decay towards 0", e.Value())
}
}
func TestVariableEWMAWarmup2(t *testing.T) {
e := NewMovingAverage(5)
testSamples := [12]float64{1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 10000, 1}
for i, f := range testSamples {
e.Add(f)
// all values returned during warmup should be 0.0
if uint8(i) < WARMUP_SAMPLES {
if e.Value() != 0.0 {
t.Errorf("e.Value() is %v, expected %v", e.Value(), 0.0)
}
}
}
if val := e.Value(); val == 1.0 {
t.Errorf("e.Value() is expected to be greater than %v", 1.0)
}
}